 ❐ Les règles du sudoku
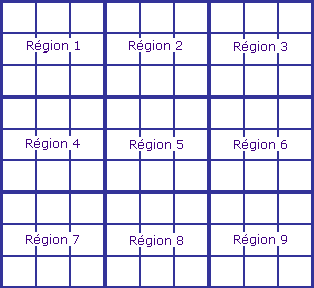
❐ Les règles du sudokuUn sudoku est un puzzle qui se présente sous la forme d'une grille de 81 cases, organisée en 9 lignes, 9 colonnes et 9 régions (carrés de 3x3 cases). Le but du jeu est de compléter la grille afin que chaque ligne, chaque colonne et chaque région contienne tous les chiffres de 1 à 9 une fois et une seule.
En principe, il n'existe qu'une seule solution pour une grille.
Il vous faudra de la logique et beaucoup de patience pour terminer les sudokus les plus difficiles.
Pour résoudre un sudoku, il est utile de noter les chiffres possibles (appelés 'candidats') dans les cases non trouvées, puis de tenter de réduire ces possibilités par diverses techniques.
❐ Techniques de résolution
Pour découvrir les techniques de résolution de soduku, lisez en français Résoudre une grille de sudoku, l'excellente page d'Angus Johnson, traduite par int24h.
Sudoku pas à pas applique les méthodes de résolution suivantes :
nb : le secteur est un nom générique pour ligne, colonne ou région
I - Recherche du candidat unique (single candidature4)
Deux méthodes simples permettent de déduire un chiffre dans une case :
-> la recherche du seul emplacement possible pour un candidat dans un secteur (hidden single1/3, single position2)
[Règle 1] Dans un secteur, si un chiffre ne peut être placé que dans une seule case, alors l'y placer.
[Règle 1] Dans un secteur, si un chiffre ne peut être placé que dans une seule case, alors l'y placer.
-> la mise en évidence du seul candidat possible dans une case (single1, single candidate2, naked single3)
Cela parait trivial, et ça l'est pour une machine, mais pas forcément pour un humain devant sa grille.
[Règle 2] Si il n'existe qu'un candidat pour une case, alors placer ce chiffre dans cette case.
Cela parait trivial, et ça l'est pour une machine, mais pas forcément pour un humain devant sa grille.
[Règle 2] Si il n'existe qu'un candidat pour une case, alors placer ce chiffre dans cette case.
Ces deux méthodes sont les seules qui permettent de déduire le chiffre à placer dans une case. Toutes les méthodes décrites ci-dessous visent seulement à diminuer le nombre de candidats dans chaque case, de façon à pouvoir appliquer efficacement une des méthodes de recherche du candidat unique.
II - Recherche d'ensembles disjoints de candidats dans un secteur (disjoint subsets4)
Le principe consiste à séparer les candidats d'un secteur en ensembles disjoints, c'est à dire qu'un candidat ne peut appartenir qu'à un seul des ensembles considérés. Pour cela il existe deux techniques générales :
-> la recherche des ensembles nus (naked subsets3)
Paire nue (naked pair1/2)
[Règle 3a] Dans un secteur, si A et B sont les seuls candidats dans deux cases, alors les candidats A et B sont absents des autres cases de ce secteur.
[Règle 3a] Dans un secteur, si A et B sont les seuls candidats dans deux cases, alors les candidats A et B sont absents des autres cases de ce secteur.
Triplet nu (naked triple1/2)
[Règle 3b] Dans un secteur, si A, B et C sont les seuls candidats dans trois cases, alors les candidats A, B et C sont absents des autres cases de ce secteur.
[Règle 3b] Dans un secteur, si A, B et C sont les seuls candidats dans trois cases, alors les candidats A, B et C sont absents des autres cases de ce secteur.
Quadruplet nu (naked quad1)
[Règle 3c] Dans un secteur, si A, B, C et D sont les seuls candidats dans quatre cases, alors les candidats A, B, C et D sont absents des autres cases de ce secteur.
-> la recherche des ensembles cachés de candidats (hidden subset3)[Règle 3c] Dans un secteur, si A, B, C et D sont les seuls candidats dans quatre cases, alors les candidats A, B, C et D sont absents des autres cases de ce secteur.
Paire cachée (hidden pair1/2)
[Règle 4a] Si deux candidats ne sont présents que dans deux cases d'un secteur, alors les autres candidats présents dans ces deux cases sont éliminés.
[Règle 4a] Si deux candidats ne sont présents que dans deux cases d'un secteur, alors les autres candidats présents dans ces deux cases sont éliminés.
Triplet caché (hidden triple1/2)
[Règle 4b] Si trois candidats ne sont présents que dans trois cases d'un secteur, alors les autres candidats présents dans ces trois cases sont éliminés. nb : les trois candidats ne sont pas forcément présents dans chacune des trois cases concernées.
[Règle 4b] Si trois candidats ne sont présents que dans trois cases d'un secteur, alors les autres candidats présents dans ces trois cases sont éliminés. nb : les trois candidats ne sont pas forcément présents dans chacune des trois cases concernées.
Quadruplet caché (hidden quad1)
[Règle 4c] Si quatre candidats ne sont présents que dans quatre cases d'un secteur, alors les autres candidats présents dans ces quatre cases sont éliminés. nb : les quatre candidats ne sont pas forcément présents dans chacune des quatre cases concernées.
[Règle 4c] Si quatre candidats ne sont présents que dans quatre cases d'un secteur, alors les autres candidats présents dans ces quatre cases sont éliminés. nb : les quatre candidats ne sont pas forcément présents dans chacune des quatre cases concernées.
Les ensembles nus pourraient être recherchés pour cinq à sept candidats, mais cette technique coûteuse revient alors à chercher des ensembles cachés de quatre, trois ou deux candidats. Et l'inverse est également vrai.
exemple 1 : {1,2,3,4,5}{1,2,3,4}{1,2,3}{2,3,4,5}{1,3,4,5}{6}{7,8}{7,9}{8,9,1}
on voit que la recherche d'un 5-uplet nu (à gauche) et la recherche d'un triplet caché (à droite) amènent le même résultat : la suppression du candidat 1 dans la dernière case.
exemple 2 : {1,2,3,4,5,9}{1,2,3,4}{1,2,3}{2,3,4,5}{1,3,4,5}{6}{7,8}{7,9}{8,9}
à l'inverse, on voit que la recherche d'un 5-uplet caché (à gauche) et la recherche d'un triplet nu (à droite) amènent aussi le même résultat : la suppression du candidat 9 dans la première case.
Les deux techniques sont donc complémentaires et il est donc inutile de rechercher les ensembles cachés et les ensembles nus d'ordre supérieur ou égal à 5.
III - Recherche des interactions entre régions (locked candidates1, single sector candidates4)
L'idée consiste à éliminer des positions d'un candidat dans une région en examinant les conséquences du placement de ce candidat dans une région alignée.
Le couloir (candidate lines2, block, column & row interactions3)
[Règle 5a] Dans une région donnée, si toutes les occurences d'un candidat sont alignées dans une ligne ou une colonne, alors ce candidat est éliminé de cette ligne ou de cette colonne dans les régions adjacentes alignées.
[Règle 5a] Dans une région donnée, si toutes les occurences d'un candidat sont alignées dans une ligne ou une colonne, alors ce candidat est éliminé de cette ligne ou de cette colonne dans les régions adjacentes alignées.
Le double couloir (multiple lines2, block / block interactions3)
[Règle 5b] Dans les régions alignées Y et Z, si toutes les occurences d'un candidat sont alignés dans deux lignes ou deux colonnes, alors ce candidat est éliminé de ces lignes ou de ces colonnes dans la troisième région alignée.
[Règle 5b] Dans les régions alignées Y et Z, si toutes les occurences d'un candidat sont alignés dans deux lignes ou deux colonnes, alors ce candidat est éliminé de ces lignes ou de ces colonnes dans la troisième région alignée.
IV - Traitement des contraintes portant sur un candidat dans toute la grille
L'idée consiste à considérer toutes les positions possibles d'un candidat sur la grille puis à rechercher les incohérences entre ces candidatures, ce qui permet d'éliminer certaines d'entre elles.
Formation en X (X-wing1/2/3/4)
[Règle 6a] Soit un candidat apparaissant aux intersections de 2 lignes et 2 colonnes; si ce candidat n'apparait pas dans d'autres cases des-dites lignes, alors il peut être eliminé dans les-dites colonnes (sauf aux intersections); si ce candidat n'apparait pas dans d'autres cases des-dites colonnes, alors il peut être eliminé dans les-dites lignes (sauf aux intersections)
[Règle 6a] Soit un candidat apparaissant aux intersections de 2 lignes et 2 colonnes; si ce candidat n'apparait pas dans d'autres cases des-dites lignes, alors il peut être eliminé dans les-dites colonnes (sauf aux intersections); si ce candidat n'apparait pas dans d'autres cases des-dites colonnes, alors il peut être eliminé dans les-dites lignes (sauf aux intersections)
Swordfish (swordfish1/2/3/4)
[Règle 6b] Soit un candidat apparaissant aux intersections de 3 lignes et 3 colonnes; si ce candidat n'apparait pas dans d'autres cases des-dites lignes, alors il peut être eliminé dans les-dites colonnes (sauf aux intersections); si ce candidat n'apparait pas dans d'autres cases des-dites colonnes, alors il peut être eliminé dans les-dites lignes (sauf aux intersections)
Il est frappant de voir les divergences de définitions du swordfish selon les sites.
Sont-elles équivalentes ?
J'ai opté pour celle d'Angus Johnson (Simple Sudoku1), facile à interprèter et à coder, mais peut-être un peu moins facile à admettre.[Règle 6b] Soit un candidat apparaissant aux intersections de 3 lignes et 3 colonnes; si ce candidat n'apparait pas dans d'autres cases des-dites lignes, alors il peut être eliminé dans les-dites colonnes (sauf aux intersections); si ce candidat n'apparait pas dans d'autres cases des-dites colonnes, alors il peut être eliminé dans les-dites lignes (sauf aux intersections)
Coloriage (solving with colors1, colouring3)
(règle non implémentée)
(règle non implémentée)
Nishio (nishio1/2/3/4)
(règle non implémentée)
(règle non implémentée)
V - Traitement des contraintes portant sur plusieurs candidats dans toute la grille
L'idée consiste à considérer les positions possibles de deux ou plusieurs candidats sur la grille puis à rechercher les incohérences entre ces candidatures, ce qui permet d'éliminer certaines d'entre elles.
Formation en XY (XY-wing3/4)
(règle non implémentée)
(règle non implémentée)
Chaine forcée (forcing chains2/3)
(règle non implémentée)
(règle non implémentée)
Les dernières méthodes présentées ne sont pas encore disponibles dans Sudoku pas à pas. Ceci dit, Sudoku pas à pas devrait vous éclairer sur la quasi-totalité des grilles parues dans la presse.
1/2/3/4 : comme d'autres 'chercheurs' inspirés par l'apparition des sudokus, j'avais mis au point mon propre vocabulaire (désignations des régions et des candidats, noms des méthodes de recherche). Constatant la cacophonie règnant à ce sujet sur le net, j'ai décidé de me rallier au vocabulaire majoritaire, d'origine anglo-saxonne. Vous trouverez donc en complément de dénominations francophones les termes utilisés sur quatre sites anglo-saxons (référencés 1/2/3/4 dans la page Liens) qui ont fait un effort de pédagogie et/ou de conceptualisation. Vous pouvez constater que les terminologies utilisées pour nommer les méthodes de recherche convergent mais restent spécifiques à chaque auteur. (2/11/05)